Shiken:JALT Testing & Evaluation SIG Newsletter
Vol. 3 No. 1 Apr. 1999. (p. 20 - 25) [ISSN 1881-5537]
PDF Version
PDF Version
Standard error vs.
|
 James Dean Brown University of Hawai'i at Manoa |
QUESTION:
One of the statistics my spreadsheet gives me is Standard Error. Is that the same as the Standard Error of Measurement?
ANSWER:
The most direct answer to your question is "no." Most likely, you are referring to the STEYX function in the ubiquitous ExcelTM spreadsheet. The statistic calculated by the STEYX function is commonly referred to as the standard error of estimate and that is not the standard error of measurement.
As your question suggests, the standard error of estimate is often confused with the standard error of measurement that is reported by some test analysis software, or even with the standard error of the mean that is reported by more sophisticated statistical packages like SPSS, SAS, or SYSTAT. Let me try to unscramble all of this step by step by first reviewing what the standard deviation is. Then I will be able to explain the definitions and differences among the standard error of the mean, the standard error of estimate, and the standard error of measurement.
Standard Deviation
As I defined it in Brown (1988, p. 69), the standard deviation "provides a sort of average of the differences of all scores from the mean." This means that it is a
measure of the dispersion of scores around the mean. The standard deviation is
related to the range (another indicator of dispersion based on the distance between
the highest and lowest score), but has the advantage over the range of not being affected as much as the range by aberrant scores that are exceptionally high or low. Generally, a low standard deviation means that a set of scores is not very widely dispersed around the mean, while a high standard deviation indicates that the scores are more widely dispersed. [For more information on calculating and interpreting standard deviations, see Brown 1988 amd 1995]
It turns out that, in a normal distribution, about 68% of the students can be expected to fall in the range of scores between minus one standard deviation below the mean and plus one standard deviation above the mean and that about 95% of the students can be expected to fall in the range of scores between minus two standard deviations below the mean and plus two standard deviations above the mean. So on a test with a mean of 51 and standard deviation of 10, you can expect about 68% of the students to score between 41 and 61, and about 95% of the students to score between 31 and 71. This use of percents with the standard deviation will become important in interpreting all three of the standard error statistics described below. Now, having reviewed the basic concept of standard deviation, it is possible to consider the concept of standard error of the mean.
Standard Error of the Mean
Conceptually, the standard error of the mean is related to estimating the population mean in that it provides an indication of the dispersion of the sampling errors when you are trying to estimate a population mean from a sample mean. In order to understand the previous sentence you will first need to understand three bits of jargon: sampling errors, population mean, and sample mean. I'll deal with them in reverse order.
Usually, you do not have the resources to measure the entire population of students when you give a test. Typically, for instance, you administer a test to a class or group of incoming students, but not to the entire school. Also in other experimental research situations, you might find yourself taking a random sample of the population of students in order to make your measurement, data entry, analysis, and other work easier. If the sample is truly random, researchers consider it representative of the population. Nonetheless, sample statistics like the sample mean, the reliability estimate for the sample, or any other statistics based on the sample are not likely to be exactly the same as those for the population. The ones for population are referred to as population parameters. Often people measure sample statistics thinking those statistics are the same as the population parameters. For instance, you might calculate the sample mean of a random sample of 50 students on some test and assume that it is the same as the population mean for that test.
[ p. 20 ]
However, if you were to select random samples of 50 students one after the other until you had 100 such random samples and administered the same test to all the students, you would find that the 100 samples would have many different means. Moreover, if you were to plot the means for the 100 random samples you would find that a histogram of those means would probably be normal in distribution and that the means themselves would have a mean (this mean of means, by the way, would probably be the best estimate of the population mean). The standard deviation of such a distribution of means is referred to as the standard error of the mean because it represents the distribution of errors (or random fluctuations) in estimating the population mean. Thus the standard error of the mean is the standard deviation for the distribution of errors or random fluctuations that are likely to occur in estimating the population mean from sample means in a particular situation. Based on the percentages discussed in the previous section for the standard deviation, we can expect about 68% of the errors to be distributed within one standard error plus or minus of the population mean, and about 95% to be distributed within two standard errors plus or minus of the population mean.
Normally, you will not have the time or resources to actually take 100 samples. Instead, you may want to use the following formula to estimate the standard error of the mean from a single sample:
Standard Error of Measurement
Conceptually, the standard error of measurement is related to test reliability in that it provides an indication of the dispersion of the measurement errors when you are trying to estimate students' true scores from their observed test scores. In order to understand the previous sentence you will first need to understand three bits of jargon: sampling errors, true scores, and test scores. I will deal with them in reverse order.
[ p. 21 ]
Students' test scores are not a mystery: they are simply the observed scores that the students got on the whatever test is being considered. However, that same students' true scores are a bit more difficult to understand. Let's say that you can give a test an infinite number of times to a group of students (I know fatigue would probably become a problem sometime before infinity, but this is just for the sake of argument). If you could average the students' scores over the infinite number of administrations, the average of each person's scores would probably be the best estimate of that person's true ability/knowledge in whatever is being tested, or that person's true score. The standard deviation of all those scores averaged across persons and test administrations is the standard error of measurement.
Of course it is humanly impossible to administer a test an infinite number of times while holding testing effect, fatigue, and other variables constant. So we settle for second best. We assume that each student's test score is our best estimate of the true score, but we recognize that there are sampling errors in that estimate, just as there were for estimating the population mean. Those sampling errors are normally distributed and have a standard deviation called the standard error of measurement.
Fortunately, an estimate of the standard error of measurement can be calculated from the test score standard deviation and reliability estimate using the following formula:
So, if you have a test with a standard deviation (S) of 4.89, and a Cronbach alpha reliability estimate (rxx) of .91, the standard error of measurement would be calculated as follows:
One useful application of the standard error of measurement is that it can be used to estimate a band of scores around any cut-point wherein students are treated with special care. For instance, if the test in question had a cut-point for failing of 30, you should recognize that, if you want to be 68% sure of your decision, the standard error of measurement indicates that the students within one (SEM) of the cut point (i.e., 30 
1.47, or 28.53 to 31.47) might fluctuate randomly to the other side of the cut point if they were to take the test again, so it might behoove you to gather additional information (e.g., other test scores, homework grades, interviews with the students, or whatever is appropriate) in deciding whether or not they should pass the test.
[ p. 22 ]
By extension, if you want to be 95% sure of your decision, the standard error of measurement indicates that the students within two (SEM)s of the cut point (i.e., 30 2.94, or 27.06 to 32.94) might randomly fluctuate to the other side of the cut point, and you may want to act accordingly. [For further explanation of the standard error of measurement, see Brown, 1996, or Brown with Wada, 1999].
Conceptually, the standard error of estimate is related to regression analysis in that it typically provides an estimate of the dispersion of the prediction errors when you are trying to predictY values from X values in a regression analysis. In order to understand the previous sentence, you will first need to understand three bits of jargon: prediction errors, Y values, and X values. Again, I would like to deal with those terms in reverse order. In a regression analysis, X values are any values from which you want to predict, and Y values are any values to which you want to predict. Unfortunately, those predictions are never perfect because prediction errors occur. Such errors may be due to unreliable measurement in either the Y or X variable, or due to unsystematic differences between the two sets of numbers. When you are trying to predict Y values from X values, it would be useful to know what the distribution of those prediction errors is so you can interpret your predictions wisely.
An example of such a situation might be a case where you use regression analysis to predict TOEFL scores from the PERFECT test at your institution. You must first conduct a study based on a large number of students who took both tests. Then using regression analysis, you build a regression equation of the form Y = a + b X. Based on your analysis, you will know the values of a (the intercept) and b (the slope), and can then plug in the X value (or PERFECT test score) for a student who has never taken the TOEFL. Solving for Y will then give you that student's predicted Y (or predicted TOEFL score). All of this is beyond the scope of this explanation, but is necessary in order to get even a basic understanding of what the standard error of estimate is. [For more on regression analysis, see Brown, 1988, or Hatch and Lazaraton, 1991].
We assume that any student's predicted Y score is our best estimate of that score, but we recognize that there are sampling errors around that estimate, just as there were for estimating the population mean and true scores. Those sampling errors are normally distributed and, in this case, have a standard deviation called the standard error of estimate.
Fortunately, you can use the following simple formula to calculate the standard error of estimate from the standard deviation of the Y values in the original regression analysis and the correlation coefficient between the X and Y values in that analysis:
[ p. 23 ]
One useful application of the standard error of estimate is that it can be used to create a band of scores around any predicted score. For instance, if a students predicted Y score is 35, the see (just calculated) of 4.08 would tell you that the student's predicted score is likely to vary within plus or minus 4.08 points on Y 68% of the time. So you know that the prediction would fall between 30.92 and 39.08 with 68% confidence. At this point, you can probably guess how you would go about establishing bands of scores for 95% confidence. Such bands of confidence intervals around predictions are very useful in making decisions based on predictions. [For further explanation of the standard error of estimate, see Brown, 1988, or Hatch and Lazaraton, 1991].
Quite obviously, the standard deviation, standard error of the mean, standard error of measurement, and standard error of estimate are quite different things. They are all based on the simple notions of the normal distribution, but they have quite different applications. In a nutshell:
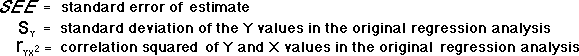
[ p. 24 ]
References
Brown, J. D. (1988). Understanding research in second language learning: A teacher's guide to statistics and research design.
London: Cambridge University Press.
Brown, J. D. (1996). Testing in language programs. Upper Saddle River, NJ: Prentice Hall.
Brown, J. D. (trans. by M. Wada). (1999). Gendo kyoiku to tesutingu. [Language teaching and testing]. Tokyo: Taishukan Shoten.
Hatch, E., & Lazaraton, A. (1991). The research manual: Design and statistics for applied linguistics. Rowley, MA: Newbury House.
Author IndexTitle IndexDate Index
Background
Links
Network
Join
[ p. 25 ]