Rasch Measurement in Language Education: Part 1 by James Sick

Shiken: JALT Testing & Evaluation SIG Newsletter
Vol. 12 No. 1 Jan. 2008 (p. 1 - 6) [ISSN 1881-5537]
PDF Version

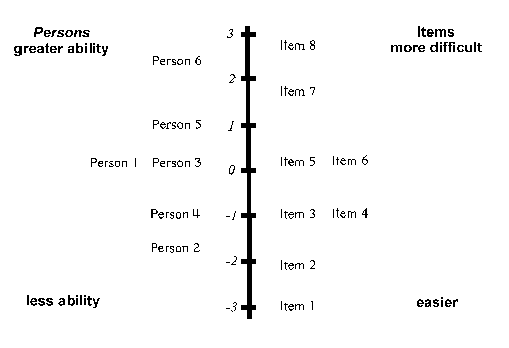
Rasch Measurement in Language Education: Part 1
James Sick, Ed.D. (J. F. Oberlin University, Tokyo)

In this multipart series, I will present the basic principles of Rasch measurement theory and discuss how it can be usefully applied in foreign language education. The first installment will compare Rasch theory to classical test theory (CTT) and Rasch theory's close relative, Item Response Theory (IRT). Future installments will examine in greater detail the various models in the Rasch family and discuss how they can be used to construct measures from diverse types of data, including dichotomously scored tests, Likert-style questionnaires, and judged performances. The column will be presented in a question and answer format. Readers who would like to submit a particular question are invited to send their inquiries to the author.

"[Rasch measurement theory can] play an important role in the process of construct validation, in that a set of test or questionnaire items constitute the instrument designer's empirical definition of the construct."

What is Rasch measurement theory?

Rasch measurement theory (RMT) refers to a family of statistical models and techniques used to assess the quality of tests and questionnaires, and to construct true interval-scale measures from the raw scores obtained from such instruments. RMT can be said to embody a theory of psychological measurement, in that it provides a set of prescriptive criteria for judging the degree to which measurement has been successful. It can also play an important role in the process of construct validation, in that a set of test or questionnaire items constitute the instrument designer's empirical definition of the construct. A Rasch analysis can be used to evaluate the degree to which responses to these items conform to what would be expected if the items were indeed measuring a single, coherent psychological attribute.

How does Rasch differ from classical test theory?

Rasch measurement differs from CTT in several appreciable ways. First, CTT is primarily concerned with total scores. Total scores, the number of items answered correctly, serve as the sole indicator of a person's level of ability or knowledge, and all items are treated as equal contributors to the total score. That is, difficult items are not weighted more highly than easier items when estimating levels of knowledge or ability. Moreover, equal differences in total scores are treated as delineating equal ranges of ability, whether they be from 40 to 50 points, for example, or from 85 to 95 points. In CTT, the primary indicator of test quality is reliability, the overall capacity of the test to define levels of knowledge or ability consistently. Reliability estimates are usually derived by comparing the total scores of one half of the test to the total scores of the other half, either directly, or indirectly using formulas such as Cronbach's alpha that approximate the mean correlation of all possible split-half combinations.
RMT, on the other hand, focuses on the pattern of item responses. A conceptual starting point is the assertion that some people have more of the attribute being measured than others, and some items require more of it to be completed successfully. Success on a difficult item implies a probable success on an easier item, and an even higher probability of success on a much easier item. A failure of the responses to confirm this hierarchical structure is regarded as a failure of measurement. In other words, a primary criteria for assessing test quality in RMT is the degree to which the items appear to be demarking a consistent, implicative progression from "requires a little" of this attribute to "requires a lot."

[ p. 3 ]

A second difference is that CTT is primarily descriptive and sample dependent. It provides a description of the data from a single administration of a test, including the reliability of that administration, and the difficulty of individual items in terms of the percentage of test takers who answered them successfully. It is acknowledged that these values will be different if the test is administered to a different group of people. In contrast, Rasch measurement is probabilistic and inferential. Although estimates of person ability and item difficulty are derived from an analysis of a particular test administration, both people and items are viewed as samples drawn from a larger population: people from the population of plausible test takers, and items from the universe of items that could potentially be employed to measure that construct. Ultimately, we seek to derive inferences and predictions, such as "a person at this level of ability is fifty percent likely to be successful at this item", or, "if an item of this difficulty were administered to fifty people at this level of this ability, it would likely be answered successfully by about twenty-five of them."

How exactly are such inferences derived?

   Future installments will discuss in greater detail how different Rasch models are applied to various measurement situations. For the moment, it will suffice to say that in the initial analysis, person ability and item difficulty are conjointly estimated and placed on a single numerical scale. Person and item measures are aligned on this scale by defining ability as the "threshold of success." That is, a person's ability measure is defined as the point on the item/attribute continuum marked by items at which he or she is fifty percent likely to either succeed or fail. The fact that both item difficulty and person ability are estimated and reported on the same scale also constitutes an important difference between Rasch measurement and classical test theory.
    Yet another important difference is that the Rasch measures, unlike total scores, can have an arbitrary origin. That is, the zero point of the constructed scale of measurement can be arbitrarily set to correspond to the mean item difficulty, the mean person ability, or even set to correspond to calibrations derived from a previous test administration. This last feature permits us to link tests that share common items or were administered to common persons to a single, comparable scale of measurement. This is the basis of the property of invariance, a core component of Rasch measurement that will be discussed at length in a future installment.
    The structure of a Rasch variable is illustrated in Figure 1, a simplified person-item "variable map." In this map, which is illustrative and not based on real data, the zero point has been arbitrarily set as the mean item difficulty. Persons 1 and 3 have estimated measures slightly above the zero point, as do items 5 and 6. Because these two persons and two items are aligned on the map, we predict that each person will be successful at one of the two items, and each item will elicit a successful response from one of the two persons. Persons 1 and 3 are more than 50 percent likely to be successful at items 3 and 4 because they are lower down the item map (easier), and less than 50 percent likely to be successful at items 7 and 8 because they are higher up the item map (more difficulty).

[ p. 4 ]

Figure 1. A simplified Rasch variable map.

How is Rasch measurement different from Item Response Theory?

Although strong proponents of the Rasch approach such as Wright (1999) have argued that Rasch measurement and IRT are fundamentally different, IRT and Rasch measurement have much in common. In contrast to CTT, both analyze the pattern of responses to individual items. Both fix persons and items to a unitary scale with an arbitrary origin. Both can be considered inferential and probabilistic in that they seek to predict how a person will respond to an item based on how he or she has responded to other items, or what responses an item will provoke if administered to a different set of people.
The chief difference between IRT and Rasch measurement is that IRT approaches sometimes incorporate two additional properties of an item when estimating person ability: the degree to which the item discriminates between high and low ability test takers, and item's susceptibility to guessing. The one-parameter IRT model considers only item difficulty and is essentially the same as the Rasch model for dichotomous data. The two-parameter IRT model considers both difficulty and discrimination, and the three-parameter model incorporates difficulty, discrimination, and the probability of guessing correctly when estimating person ability.

[ p. 5 ]

"it can be argued that Rasch measurement is applicable to a wider range of measurement domains than IRT."

    In clarifying the difference between these two approaches, it can be helpful to draw a distinction between the Rasch model, Rasch measurement theory, and a Rasch analysis. The Rasch model refers to several variants of an equation that equates the probability of success to the gap between a person's ability and an item's difficulty. The dichotomous Rasch model is equivalent to the one-parameter IRT model and despite objections from some quarters, the terms are often used interchangeably. IRT regards the one-parameter (Rasch) model as appropriate when guessing is not possible and most items have similar discrimination, or when the sample size is inadequate for estimating these additional parameters. Rasch measurement theory, however, views the Rasch model as a mathematical description of ideal measurement, if we were able to achieve it (Rasch, 1960; Wright & Stone, 1979). Real world data are expected to deviate from the ideal due to random measurement error, systematic bias, less than perfect item design, and/or poor definition of the construct. A Rasch analysis examines the differences between the data and the standard set by the model in order to obtain actionable insight into how the instrument or understanding of the construct can be improved. In contrast, an IRT analysis attempts to make the best possible estimate of person ability by applying the model that best explains the variance in the item response data.
    Finally, it can be argued that Rasch measurement is applicable to a wider range of measurement domains than IRT. Two and three parameter IRT models are mainly applicable to dichotomously scored multiple-choice tests. Variations of the standard Rasch model can be applied to dichotomously scored tests, Likert-style rating scales, subjectively judged written or spoken performances, as well as items given partial credit when some but not all of the steps have been successfully completed.
    Part 1 of this series has attempted to situate Rasch measurement theory in the broader context of classical test theory and item response theory. Future installments will take a more in-depth look at how Rasch measurement can be applied to different types of measurement tasks, and the role of Rasch analysis in the process of instrument and construct validation.

References

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: Denmarks Paedagogiske Institut.

Wright, B. D. (1999). Fundamental measurement for psychology. In S. E. Embretson & S. L. Hershberger (Eds.), The New Rules of Measurement. Mahwah, NJ: Lawrence Erlbaum.

Wright, B. D., & Stone, M. H. (1979). Best test design. Chicago: MESA Press.

NEWSLETTER: Topic Index

Author Index

Title Index

Date Index
TEVAL SIG: Main Page

Background

Links

Network

Join