Testing the test: Using Rasch person scores by H. P. L. Molloy

Shiken: JALT Testing & Evaluation SIG Newsletter
Vol. 13 No. 3 Nov. 2009 (p. 6 - 12) [ISSN 1881-5537]
PDF Version

ITesting the test: Using Rasch person scores

by H. P. L. Molloy (Toyo University Faculty of Business Administration)

Abstract

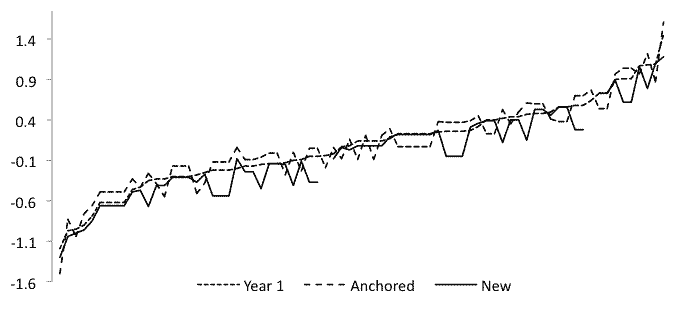
The results of analyzing a set of tests used for measuring classroom progress in EFL reading are reported. Some 353 students in Japanese university English classes took one of four tests in 2008 and 2009. Student ability scores were derived using three analytic situations: all students together, 271 students from 2008 only, and 82 students from 2009 scored with items anchored at levels set the previous year. Student scores differed noticeably in the three analytic situations, showing that item linking is necessary for intergroup comparisons. In other words, if you're not using the same tests, you cannot compare students.

Keywords: language testing, Rasch measurement, test-score correlation, classroom testing, criterion-referenced testing, test-item linking

In 2008, Christopher Weaver and I began a testing program in our EFL reading classes designed to measure first- and second-year students' progress (or lack thereof) in their reading classes. We hold that the purpose of the reading classes is to improve students' future ability to read in English and designed a testing regime for that purpose. Likewise, we aimed our teaching in that direction: to help students learn the skills they would need to deal with written English materials in the future. Our grading as well reflected this testing approach: students were rewarded not only for doing well on the tests, but also for improving their scores on the tests as the semester progressed.

The testing regime, which is explained in detail in Molloy & Weaver, 2009 and Molloy, 2009, is simple and can be used by any classroom teacher tasked to improve students' skills. Also, our approach to planning and test making was likely closely akin to what many L₂ teachers do. First, the content of the course is decided. This we did largely by simply thinking of reading problems (e.g., dealing with unknown or newly coined lexicogrammatic items) and deciding (each of us separately) how the skills to deal with them should be taught. That is, we set goals for our classes, but did not prescribe any teaching method. The tests comprised items (i.e., test questions) designed to test the ability to deal with those problems. The text passages used in the tests were extracts from descriptive nonfiction books because of our students were business administration majors who would, presumably, have futures in widely varied industries. Rather than teaching sundry specialized lexicogrammatic fields, we felt if wiser to teach a preselected group of frequent words or commonly used rhetorical patterns.

In essence, we were applying some of the aspects of norm-referenced testing (e.g., with the TOEIC^® test) to classroom-based criterion-referenced testing. This is because of a concern for measuring progress in learning English: as with norm-referenced testing, in which the concern of the test user is to compare particular language users with others and find the best or the worst, the test regime described here compares test takers with earlier versions of themselves. Conventional norm-referenced tests such as the TOEIC work by checking how many and which questions or items students can successfully complete with how many and which other test takers succeed at and use that information to rank the test takers. The tests described in this paper were designed for comparing test takers with their earlier selves by checking how many and which items they could succeed at and comparing the results with results obtained for other students at earlier times.

The problem remains, however, of how to actually test changes in reading skill: the tests we developed were entirely new and of unknown difficulty. It seemed likely that students would exhibit different patterns of change in reading ability at different rates. If we gave all our students the same tests at the same time, we would not be able to measure progress because we wouldn't know if, for example, students were getting higher scores because their reading skills were improving or because the tests were becoming easier.

[ p. 6 ]

We addressed this problem by counterbalancing the tests we developed over time and over students. We made four tests. Then, as a level-check exercise, gave a more-or-less randomly selected (see Molloy & Weaver, 2009a, 2009b) one-quarter of the students each of the tests. This allowed us to establish the difficulties of the items that made up the tests. We then anchored the item difficulties at the values determined during the first (level-check) administration for subsequent administrations, which allowed us fixed scales against which to measure student progress. We further worked against test content effects by having students take all of the tests in different orders at four different occasions during the semester, so that while one quarter of the students were taking one particular test on every testing occasion, the composition of those one-quarters of students was different at each test administration. Permuting 4 tests for administration order yields 24 unique orders of tests, and every class had, at most, two students taking the tests in any one particular order.

As a matter of course, we used the Rasch model and Rasch analysis software (Winsteps Ver. 3.64.0, Linacre, 2007), but the advantage of this approach (leaving aside the aptness of the analytic approach) its convenience: for the uses to which we put our data, classical test analyses would have been just as effective (as explained in Molloy & Weaver, 2009b).

Meanwhile, for our Spring 2009 semester listening classes, we developed an analogous set of tests administered under an analogous scheme. Because some of our students also took the Fall reading classes, we could compare the scores and see what differences obtained. That comparison will be the theme of a later article. This article instead focuses on item difficulty score differences in the same set of tests.

How this Study was Done

We have continued with the reading testing program by giving the same tests to students from a second year. Now, we can test the tests by seeing if they yield student scores that are the same in three different cases. Case A is when the student scores are started afresh, as if the test had never been given before and the item difficulties were unknown. Students in this test situation are called "New" in this article. Case B is when students from the Fall 2009 semester are scored according to the item difficulties determined during test administration during the Fall 2008 semester. These students are called "Anchored." Case C is when the students from the Fall 2009 semester are treated as if they took the test at the same time as the students from the Fall 2008 semester. This is the "Year 1" testing situation.

Mind, I am dealing here with what happens to one single set of test responses when they are analyzed in three different analytic situations (here called "testing situations"). These are the "New," "Anchored," and "Year 1" cases. Even though there are cases in which students' ability scores differ, the scores discussed represent exactly the same responses to the tests. That is, we will see students' scores change simply because of which other students are included in the analyses.

Why the Study was Done

The Rasch model is built on the assumption that raw test scores are adequate measures of ability for whatever that test is designed to measure, provided that the items on the test are adequately differentiated on a scale of difficulty. However, in practice, the Rasch model is often used in analytic procedures (such as the one we undertake here) when test users have no solid evidence of the relative difficulty of the particular items. In such analytic procedures, test item difficulty is estimated empirically by calculating the odds of test takers of various abilities successfully responding to given questions. Basically, if a lot of students answer a question correctly, that question is placed at the easy end of the scale. Conversely, if only a few students answer successfully, the question is considered difficult.

Simultaneously, the ability of the test takers is being estimated in the same procedure. Depending on how many and which questions a student successfully answers, he or she is ranked as more or less able.

[ p. 7 ]

Rasch analytic approaches yield "person-free item estimates" and "item-free person estimates." That is, items will be measured as equally difficult no matter what the ability of the people who respond to those items and people will be measured as equally able no matter which items they respond to. This may seem counterintuitive, but Rasch analysis of tests is based on the interplay of persons and items, essentially defining one in terms of the other.

But, butÉ. Classroom teachers usually deal with small numbers of students and small numbers of items. The person abilities and item difficulties are simultaneously estimated from a relatively small set of data. For example, in this study, our four tests had 30 items each. The tests were taken by about 90 students each. This means that our item difficulties and person abilities for each test were derived from a mere 2,700 or so data points only. Can we really trust the estimates? After all, the students for the most part already had been streamed by ability both by themselves in selecting the particular university they did (see Molloy & Shimura, 2006) and by the TOIEC-IPT test. Other sources, then, tell us the students in this study are more or less the same in ability, yet our Rasch analysis allows us to differentiate between them. Should we really trust the analysis?

Similarly, Rasch analyses yield "rulers" with which we can measure items and persons. The rulers are calibrated in terms of item difficulty and person ability. If we have a person of ability x and an item of difficulty x, we know that the person has a 50% chance of answering the item correctly. (The 50% can be adjusted, but usually it's set at 50%.) Because the items and the people are measured against the same ruler, we can use the ruler for other cases. For example, if we give the same test for a new bunch of students, we can directly compare the abilities of the new students with the abilities of the students who took the test at another time. Similarly, we can give the same students a new set of test questions and estimate the difficulty of the new questions, which allows us to directly compare the new items and the old items. That is, if we know the difficulty of questions for one group of students, we should know the relative difficulty of the same questions for a different group of students. Likewise, if we know the abilities of a group of students who have faced one set of test items, we should know the relative difficulty of a different set of items, provided the items test the same skill. The analyses, then, are person-free and item-free, but are the "rulers" situation free? This is the question I consider here.

Luckily, our using the same test two years running with two sets of students determined (by the TOEIC-IPT test) to be of different English ability levels allows us to test the adequacy of the student ability estimates, and this is what we did.

Procedure

How this Study was Done

A total of 353 first-year students from two different universities in Japan took one of the four reading tests. None of the students were English majors, and all were in required English classes. All were proficient in Japanese, though some had Japanese as a non-first language or held non-Japanese passports. Table 1 shows a breakdown of how many students took each test at which time.

Table 1. Number of students who took each test on each occasion
Occasion	Test A	Test B	Test C	Test D
Fall 2008	70	65	67	69
Fall 2009	19	20	19	24
Total	89	85	86	93

Materials

The texts in the tests were taken or adapted from a popular science book on sharks (Lineaweaver III & Backus, 1970) (Test A), a population genetics textbook (Hartl, 1981) (Test B), a introductory biology textbook (Gould & Keeton, 1996) (Test C), and a book on symmetry (Gardner, 1982) (Test D). Each test contained three excerpts from one book and one further short passage. This further short passage was a casual (Eggins, 1994) English rewriting of one of the passages from the books.

[ p. 8 ]

Hence, each test comprised two passages each from a popular science book written for proficient English users and questions about each of the passages. Each test also included one further book excerpt alongside a passage conveying the same information rewritten in a non-formal style (e.g., Eggins, 1994).

Each test comprised 30 questions we thought relevant for our students' future English use and tested the ability to use skills we planned to teach during the semester. All of the questions were written in both Japanese and English. All of the responses were in multiple-choice format. Many of the question responses (excluding those in which Japanese would have given away the answer) were in both Japanese and English, as well. We used bilingual questions and responses because our focus was on testing students' ability to deal with the test texts, not their ability to understand questions about the text. We did not want to burden students with the extra difficulty of understanding what the test items were about.

We are still using the tests and so because of test security do not wish to reproduce the test questions here. However, the ersatz examples below give some idea of the flavor of the items on the tests. For these items, please imagine that text consisted of the first three paragraphs of the "Materials" section in this paper.

Test administration

We gave the tests during the first session of class. Students were allowed as long as 1 hour to finish the tests. Students who missed the first class took the test during the second class session or whenever they first came to class. Students were informed that the tests were difficult and were designed to test the skills to be taught during the classes.

Analyses

Five major steps were involved in the analyses.

First step: Setting anchor scores. We used the item difficulty scores from the initial testing ("Fall 2008") as anchor scores in a Winsteps input file for later administrations of the tests. This was necessary if the tests were to be used to measure changes in reading skill.

Second step: Sorting data into three groups. For the initial tests in the following ("Fall 2009") reading courses, I analyzed scores in the same way, but put them into three kinds of Winsteps input file. One kind (called "Year 1" here) included all of the students who had taken a test as a level check, putting students from two academic years together. This was treating all of the tests as if they had been given simultaneously. The numbers of students in these files matched the numbers in the "Total" row of Table 1.

[ p. 9 ]

Another kind of file ("Anchored") contained only responses from the second batch students (with ns like the "Fall 2009" row in Table 1) with the item difficulties anchored at the levels derived from the first test administration. This, again, was treating the tests as if they were made of items of perfectly known difficulty and simply measuring the Fall 2009 students against that difficulty scale.

The last kind of file ("New") contained only responses from Fall 2009 students (with ns like the "Fall 2009" row in Table 1) with no item difficulties at all, so that the Winsteps program was forced to analyze the item difficulties anew. The number of students used in these analyses was the same as with the Anchored analyses.

In all cases, I set the mean person score at 0 and one logit at 1, so a score of, say, 0.5 is pretty good and one of -0.5 not so good, with the average being, of course, 0. The three types of input files were run through Winsteps (so I ran Winsteps 12 times, 3 times for each test), and I collected the student ability scores for each Fall 2009 student from each run of Winsteps.

These ability scores were the data used for the analyses described next.

Third step: Analysis of sorted groups. Basically, I analyzed the test responses of the Fall 2009 students in three contexts, as detailed above: as if they took the test in Fall 2008 with all the other students (Year 1), as if they were being measured against the item difficulties determined in the Fall 2008 testing (Anchored), and as if they were the first students to have used the test (New). To check if the students were being measured the same way in all three test situations, I simply figured correlation coefficients for the students' scores in all three situations. I calculated both parametric (Pearson's r) and nonparametric (rank-order) (Spearman's ρ and Kendall's τ) correlation coefficients.

Fourth step: Checking differences in students' scores. While arranging the output of the various Winsteps runs in a spreadsheet, I noticed that the scores output from the different testing situations seemed to differ substantially, so that, for example, one student might receive scores of 0.47 (Year 1), 0.61 (anchored), and 0.15 (new). For this reason, I decided to check just how far students' absolute scores differed among the different test situations. I found the mean difference in scores for each of the three possible pairings.

Note that I did not attempt to include measurement error in the calculations. Because the number of students and, especially, the number of items were small, error was relatively large (viz, about 0.4 for most student ability scores, meaning that a student with a score of 0 might be considered to have a roughly 95% chance of scoring from -0.4 to +0.4 on a test of the same skills that is of the same difficulty). The situation, however, was a classroom testing one. At some point, I had to set some sort of decision point(s). In this case, I simply made the decision points coincident with ability scores. In higher stakes situations, my approach might be different.

Results

The results of the score correlations were encouraging. For all the testing situations, students could be ranked in substantially the same way, despite the imprecision necessarily attendant on such a short test. Table 2 shows the correlations for each combination of testing situations for each class.

Table 2. Correlation coefficients for test scores under three testing situations for the same students
	Year 1-anchored			Year 1-new			Anchored-new
	r	ρ	τ	r	ρ	τ	r	ρ	τ
Class A (n=39)	0.95	0.96	0.86	0.97	0.95	0.85	0.90	0.90	0.75
Class B (n=35)	0.95	0.97	0.96	0.85	0.97	0.86	0.91	0.92	0.76

[ p. 10 ]

Score differences under each of the three testing situations appear in Table 3. This shows the mean difference in Winsteps ability scores for the students in each of the classes. We might consider higher scores to a difference of the placement of the ruler vis-à-vis some unknown "real" ruler's center. For the purposes of the Winsteps runs, persons were always centered at zero, so any differences seen in Table 3 can be attributed to a sample-dependent moving of the center of the ruler with relation to rulers derived from the other testing situations. Perhaps we might conceive of a hypothetic "real" ruler (perhaps created with and encompassing the abilities of all English-using readers) in relation to which the rulers in each of the testing situations is placed relatively high or low.

Table 3. Average absolute deviations of Winsteps ability scores for each class under each combination of testing situations
	Year 1-anchored	Year 1-new	Anchored-new
Class A (n=39)	0.14	0.11	0.21
Class B (n=35)	0.13	0.10	0.21

Figure 1 gives a bit more detail in a manner that may be more illuminating for some. To make the graph, I simply ordered the scores from 78 students from lowest (on the left) to highest (right). Note that the solid line, which represents the scores from the New testing situation, is generally lower than the other two curves. The line tending to be on top represents the Anchored scores, and the scores roughly in the center are the Year 1 scores.

It is easy to see that the New testing situation tends to yield lower scores and the Anchored higher, implying that the students from the Fall 2009 classes tended to be more able than those from the Fall 2008 classes.

Figure 1. Curves showing the tendency of the 3 test situations to rank students as more or less able compared. (n = 78)

Please note that the x axis in Figure 1 represents person scores. The x axis is meaningless because scores are simply arranged along the x axis from left to right by ascending score in the Year 1 situation.

Discussion

The correlation coefficients are encouraging. They seem to show that the tests are putting students pretty much in the same place no matter what testing situation is used. We can say "student A is more able than student B" with some confidence. This is true if the errors are not so large that student ability scores do not overlap.

[ p. 11 ]

The information on deviations is sobering. The correlation coefficients show students are being ranked fairly consistently. However, we can see that, without some information linking groups of students, we cannot tell if, for example, the top student from one class (say, Mr. Suzuki) is more skilled than the top student (say, Ms. Takakusagi) from another class. What happened here was, even though different students were taking the same test, the context of the other students' responses being included in the test analyses affects their scores. If Mr. Suzuki scored, say, +1 when analyzed along with the other students in his class and Ms. Takakusagi a +0.56 with those in hers, we might still find that Ms. Takakusagi is ranked higher than Mr. Suzuki if scores from her class are analyzed with Mr. Suzuki's class'. Luckily, estimating item difficulties from one group of students and using those difficulties for other students allows us just such linking. Were I to give the test at another university, I would be happy to say the students at that university were better than, worse than, or just the same as students at my own. This I would say, however, only if I gave the same test to all the students and fixed item difficulty scores to those derived from one set of students. If I were giving separate tests to students in different universities, for example, I would not feel confident in ranking students from different groups. Note, however, that the tendency for scores to float about that is most clearly understandable from the curves in Figure 1 implies there is no "real" central ability score (and, because of the way Rasch analyses work, that there is no "real" average item difficulty). In Figure 1, the "Anchored" scores generally are higher than the other two test situations, meaning that the items were more difficult for the Fall 2008 students than for the Fall 2009 students. If the items were equally difficult for the students from both years, all three lines would fall in roughly the same spots. Again, because of the way Rasch analyses work to fit data to the Rasch model, we can assume item estimates for the three test situations will evince similarly situated sets of lines on a graph. This we will see in a subsequent report.

References

Eggins, S. (1994). An introduction to systemic functional linguistics. London, England: Pinter.

Gardner, M. (1982). The ambidextrous universe: Left, right, and the fall of parity (2nd ed.). Harmondsworth, Middlesex, England: Penguin.

Gould, J. L., & Keeton, W. T. (1996). Biological science, (6th ed.). New York, NY: W. W. Norton & Co.

Hartl, D. L. (1981). A primer of population genetics. Sunderland, MA: Sinauer Associates.

Linacre, J. M. (2006). Winsteps Ver. 3.64.0 (Computer software). Chicago, IL: Author.

Lineaweaver III, T. H., & Backus, R. H. (1970). The natural history of sharks. New York, NY: Lyons & Burford.

Molloy, H. P. L., & Shimura, M. (2006, June 25). Comparing approaches to proficiency assessment problems facing faculty. Paper presented at the JACET Kanto Regional Meeting, Tokyo, Japan.

Molloy, H. P. L., & Weaver, C. (2009). Approaching the linking problem in classroom testing. In Proceedings of the 2009 Temple University Applied Linguistics Colloquium. In press.

Molloy, H. P. L. (2009). Gakusei no eigo nouryoku jyoutatu no sokutei [Measuring English student ability changes]. Touyou Daigaku Keieigakubu Nensi [Toyo University Department of Business Administration Research Annual], 2009 (forthcoming).

Newsletter: Topic Index

Author Index

Title Index

Date Index
TEVAL SIG: Main Page

Background

Links

Network

Join